
分析 (1)由题意只需证明l和AB垂直即可,由斜率公式可得l和AB的斜率,乘积为-1即可;
(2)可得直线l在y轴上的截距b=-$\frac{1}{k}$,由1<k<$\sqrt{2}$和不等式的性质可得.
解答 解:(1)∵直线l经过点P(1,0)和AB的中点(-$\frac{1}{{k}^{2}-1}$,-$\frac{k}{{k}^{2}-1}$),
∴只需证明l和AB垂直即可,由斜率公式可得l的斜率为$\frac{-\frac{k}{{k}^{2}-1}-0}{-\frac{1}{{k}^{2}-1}-1}$=$\frac{1}{k}$,
直线的AB的斜率为$\frac{-\frac{2k}{{k}^{2}-1}-0}{0-(-\frac{2}{{k}^{2}-1})}$=-k,由$\frac{1}{k}$(-k)=-1可知直线垂直,
∴A,B关于直线l对称;
(2)由(1)可知l的斜率为$\frac{1}{k}$,故l的方程为y=$\frac{1}{k}$(x-1),
可得直线l在y轴上的截距b=-$\frac{1}{k}$,
∵1<k<$\sqrt{2}$,∴$\frac{\sqrt{2}}{2}$<$\frac{1}{k}$<1,∴-1<-$\frac{1}{k}$<-$\frac{\sqrt{2}}{2}$
∴直线l在y轴上的截距b的取值范围为(-1,-$\frac{\sqrt{2}}{2}$)
点评 本题考查直线的对称轴和直线的垂直关系,涉及直线的截距和不等式的性质,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
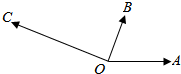 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )| A. | x=-2,y=-1 | B. | x=-2,y=1 | C. | x=2,y=-1 | D. | x=2,y=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个 | B. | 有且只有两个 | C. | 有且只有三个 | D. | 有且只有四个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com