
 a,所以在等腰△BCF中,求出EF=
a,所以在等腰△BCF中,求出EF= a.在△ABC中,利用中位线得EH∥AB,所以∠FEH或其补角就是EF和AB所成的角.最后在△EFH中,根据HE=HF=a,EF=
a.在△ABC中,利用中位线得EH∥AB,所以∠FEH或其补角就是EF和AB所成的角.最后在△EFH中,根据HE=HF=a,EF= a,利用余弦定理,可得cos∠FEH=
a,利用余弦定理,可得cos∠FEH= ,所以∠FEH=45°,从而得到正确答案.
,所以∠FEH=45°,从而得到正确答案.
 •2a=
•2a= a,同理可得CF=
a,同理可得CF= a,
a, a,BC=2a,E是BC中点
a,BC=2a,E是BC中点
 a
a =
= ,可得∠FEH=45°
,可得∠FEH=45°

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
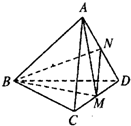 8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
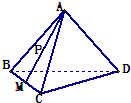 在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4
在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4| 2 |
| A、①② | B、①③ | C、②③ | D、①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com