
【题目】如图,动点![]() 到两定点
到两定点![]() 、
、![]() 构成
构成![]() ,且
,且![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与轨迹
,与轨迹![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.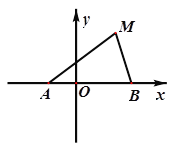
【答案】(1)3x2-y2-3=0(x>1);(2)![]()
【解析】
试题(1)首先由题意可知,显然![]() ,当
,当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,
时,![]() ,可将
,可将![]() 转化为正切值即斜率之间的关系,从而可以得到
转化为正切值即斜率之间的关系,从而可以得到![]() ,
,![]() 所满足的关系式,即可得到轨迹方程
所满足的关系式,即可得到轨迹方程![]() :
:![]() ,即
,即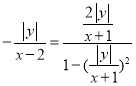 ,化简可得,
,化简可得,![]() ,而点
,而点![]() 也在曲线
也在曲线![]() ,轨迹
,轨迹![]() 的方程为
的方程为![]() ;(2)首先将直线方程
;(2)首先将直线方程![]() 与轨迹
与轨迹![]() 的方程
的方程![]() 联立,消去
联立,消去![]() 并化简后可得:
并化简后可得:![]() ,故若设
,故若设![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,则问题等价于在
,则问题等价于在![]() 有两个大于
有两个大于![]() 的根
的根![]() ,
,![]() ,且
,且![]() 的条件下,求
的条件下,求![]() 的取值范围,因此首先根据方程
的取值范围,因此首先根据方程![]() 有两个大于
有两个大于![]() 的正根,可求得
的正根,可求得![]() 的取值范围是
的取值范围是![]() ,再由求根公式,可将
,再由求根公式,可将![]() 表示为关于
表示为关于![]() 的函数关系:
的函数关系: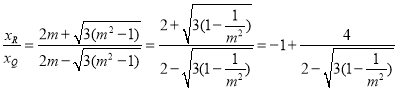 ,在
,在![]() 下,可得
下,可得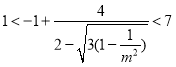 ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)设![]() 的坐标为
的坐标为![]() ,显然有
,显然有![]() ,且
,且![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,
时,![]() ,由
,由![]() ,
,
有![]() ,即
,即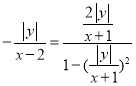 ,化简可得,
,化简可得,![]() ,而点
,而点![]() 也在曲线
也在曲线![]() ,
,
综上可知,轨迹![]() 的方程为
的方程为![]() ;
;
(2)由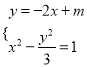 ,消去
,消去![]() 并整理,得
并整理,得![]() ,
,
由题意,方程![]() 有两根且均在
有两根且均在![]() 内.设f(x)=x2-4mx+m2+3,
内.设f(x)=x2-4mx+m2+3,
∴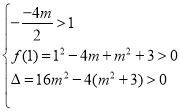 ,解得
,解得![]() ,且
,且![]() ,
,
又∵![]() ,∴
,∴![]() ,设
,设![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,由
,由![]() 及方程
及方程![]() 有
有
![]() ,
,![]() ,
,
∴ ,
,
由![]() ,得
,得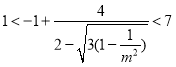 ,
,
故![]() 的取值范围是
的取值范围是![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】仔细观察数列给出部分的数字,寻找规律,在空白处填上合适的数字.
(1)2,3,5,8,__________21;(2)8,_______14,17,20,23;
(3)2,4,8,16,_______,64;(4)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,_________.
,_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
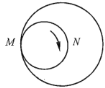
【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A.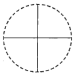 B.
B.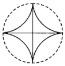 C.
C.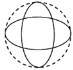 D.
D.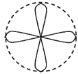
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>0,0≤x<2π,若函数y=cos2x-asinx+b的最大值为0,最小值为-4,试求a与b的值,并求使y取得最大值和最小值时的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]() 与
与![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)

(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
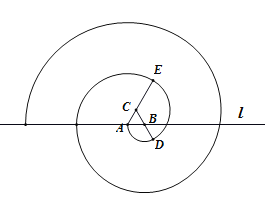
【题目】原始的蚊香出现在宋代.根据宋代冒苏轼之名编写的《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线![]() 上取长度为1的线段
上取长度为1的线段![]() ,做一个等边三角形
,做一个等边三角形![]() ,然后以点
,然后以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,以此类推,当得到的“螺旋蚊香”与直线
,以此类推,当得到的“螺旋蚊香”与直线![]() 恰有
恰有![]() 个交点时,“螺旋蚊香”的总长度的最小值为( )
个交点时,“螺旋蚊香”的总长度的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com