
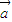 ,
,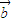 均为非零向量,(
均为非零向量,(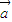 +2
+2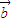 )⊥
)⊥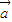 ,(
,( +2
+2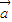 )⊥
)⊥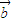 ,则
,则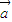 ,
,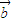 的夹角为( )
的夹角为( )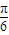
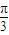
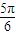

科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第51期 总207期 北师大课标版 题型:044
已知a,b均为非零向量,设a与b的夹角为![]() ,问是否存在
,问是否存在![]() ,使得|a+b|=
,使得|a+b|=![]() |a-b|成立?若存在,求出
|a-b|成立?若存在,求出![]() 的值;若不存在,说明理由.(提示:x2≥
的值;若不存在,说明理由.(提示:x2≥![]()
![]() x≥
x≥![]() ,或x≤-
,或x≤-![]() )
)
查看答案和解析>>
科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:013
设a=(x1,y1),b=(x2,y2),a、b均为非零向量,则下列命题中错误的是( ).
A.|a|=![]()
b2=![]()
a·b=x1x2+y1y2
a∥b![]() x1y2=x2y1
x1y2=x2y1
查看答案和解析>>
科目:高中数学 来源: 题型:
A.a=b B.|a|=|b| C.a⊥b D.|a|=|b|且a⊥b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com