以知{an}前项n和sn=2an-1(n∈N),(1)证明{an}是等比数列;(2)求{an}通项公式;(3)求{an}前n项的和.
解:(1)∵s
n=2a
n-1,s
n-1=2a
n-1-1,(n≥2),
∴两式相减得:s
n-s
n-1=a
n=(2a
n-1)-(2a
n-1-1),
∴a
n=2a
n-1(n≥2),即
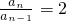
,
又令n=1,得到s
1=a
1=2a
1-1,解得:a
1=1,
同理令n=2,得到a
2=2,此两项满足此关系,
则数列{a
n}为等比数列;(5分)
(2)由(1)得到{a
n}为首项是1,公比为2的等比数列,
∴通项公式为a
n=a
1q
n-1=2
n-1;
(3)由(1)得到{a
n}为首项是1,公比为2的等比数列,
则前n项和公式s
n=
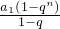
=
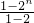
=2
n-1.
分析:(1)由已知的前n项和公式S
n,当n大于等于2时,得到S
n-1,然后两式相减,利用递推式S
n-S
n-1=a
n,得到a
n=2a
n-1,得到当n大于等于2时后项与前项之比为2,最后分别令n=1和2,求出a
1和a
2的值,验证也满足后项与前项之比为2,从而得到此数列为等比数列;
(2)由(1)得出此数列为首项是1,公比是2的等比数列,写出其通项公式即可;
(3)同理,由(1)得出此数列为首项是1,公比是2的等比数列,写出其求和公式即可.
点评:此题考查了等比数列的确定,等比数列的通项公式,以及等比数列的前n项和公式,灵活运用数列的递推式S
n-S
n-1=a
n(n≥2)是确定等比关系的关键.

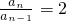 ,
,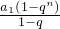 =
=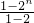 =2n-1.
=2n-1.

 名校课堂系列答案
名校课堂系列答案