
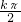 +
+ ,
,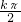 +
+ ](k∈Z).
](k∈Z).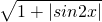 ,即y=|sinx|+|cosx|=
,即y=|sinx|+|cosx|=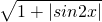 ,
, ,
, ]内,函数y=|sin2x|的减区间为[
]内,函数y=|sin2x|的减区间为[ ,
, ],
],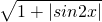 的单调减区间为:[
的单调减区间为:[ +
+ ,
, +
+ ](k∈Z).
](k∈Z). +
+ ,
, +
+ ](k∈Z).
](k∈Z).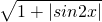 是难点,也是解决问题的关键,突出考查转化思想与分析运算能力,属于难题.
是难点,也是解决问题的关键,突出考查转化思想与分析运算能力,属于难题. 

科目:高中数学 来源: 题型:
 如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )
如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com