
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概率 | 0.32 | 0.28 | 0.18 | 0.12 |
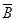 )=1-P(B)计算即可.
)=1-P(B)计算即可.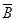 表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得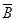 )=1-P(B)=1-0.78=0.22.
)=1-P(B)=1-0.78=0.22.

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
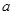 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为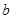 .求关于
.求关于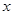 的一元二次方程
的一元二次方程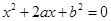 有实根的概率;
有实根的概率; 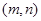 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域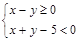 内的概率.
内的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.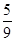 | B.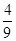 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高 | 1.81 | 1.79 | 1.79 | 1.81 | 1.79 | 1.81 | 1.77 | 1.76 | 1.83 | 1.77 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
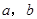 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“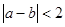 ”,其中
”,其中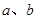 为实常数.
为实常数.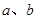 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;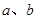 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.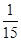 | B.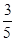 | C.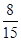 | D.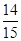 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com