
已知函数![]() 的周期为
的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数; 若不存在,说明理由.
的个数; 若不存在,说明理由.
(3)求实数![]() 与正整数
与正整数![]() ,使得
,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
本小题主要考查同角三角函数的基本关系.三角恒等变换.三角函数的图像与性质.函数.函数的导数.函数的零点.不等式等基础知识,考查运算求解能力.抽象概括能力,考查函数与方程思想,数形结合思想,分类与整合思想.化归与转化思想,满分14分.
解:(Ⅰ)由函数![]() 的周期为
的周期为![]() ,
,![]() ,得
,得![]()
又曲线![]() 的一个对称中心为
的一个对称中心为![]() ,
,![]()
故![]() ,得
,得![]() ,所以
,所以![]()
将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变)后可得
倍(纵坐标不变)后可得![]() 的图象,再将
的图象,再将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]()
(Ⅱ)当![]() 时,
时,![]() ,
,![]()
所以![]()
问题转化为方程![]() 在
在![]() 内是否有解
内是否有解
设![]() ,
,![]()
则![]()
因为![]() ,所以
,所以![]() ,
,![]() 在
在![]() 内单调递增
内单调递增
又![]() ,
,![]()
且函数![]() 的图象连续不断,故可知函数
的图象连续不断,故可知函数![]() 在
在![]() 内存在唯一零点
内存在唯一零点![]() ,
,
即存在唯一的![]() 满足题意
满足题意
(Ⅲ)依题意,![]() ,令
,令![]()
当![]() ,即
,即![]() 时,
时,![]() ,从而
,从而![]() 不是方程
不是方程![]() 的解,所以方程
的解,所以方程![]() 等价于关于
等价于关于![]() 的方程
的方程![]() ,
,![]()
现研究![]() 时方程解的情况
时方程解的情况
令![]() ,
,![]()
则问题转化为研究直线![]() 与曲线
与曲线![]() 在
在![]() 的交点情况
的交点情况
![]() ,令
,令![]() ,得
,得![]() 或
或![]()
当![]() 变化时,
变化时,![]() 和
和![]() 变化情况如下表
变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当![]() 且
且![]() 趋近于
趋近于![]() 时,
时,![]() 趋向于
趋向于![]()
当![]() 且
且![]() 趋近于
趋近于![]() 时,
时,![]() 趋向于
趋向于![]()
当![]() 且
且![]() 趋近于
趋近于![]() 时,
时,![]() 趋向于
趋向于![]()
当![]() 且
且![]() 趋近于
趋近于![]() 时,
时,![]() 趋向于
趋向于![]()
故当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 内有无交点,在
内有无交点,在![]() 内有
内有![]() 个交点;
个交点;
当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 内有
内有![]() 个交点,在
个交点,在![]() 内无交点;
内无交点;
当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 内有
内有![]() 个交点,在
个交点,在![]() 内有
内有![]() 个交点
个交点
由函数![]() 的周期性,可知当
的周期性,可知当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 内总有偶数个交点,从而不存在正整数
内总有偶数个交点,从而不存在正整数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 在
在![]() 内恰有
内恰有![]() 个交点;当
个交点;当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 在
在![]() 内有
内有![]() 个交点,由周期性,
个交点,由周期性,![]() ,所以
,所以![]()
综上,当![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 内恰有
内恰有![]() 个零点
个零点


科目:高中数学 来源:2012-2013学年安徽省合肥168中、屯溪一中高三(上)12月联考数学试卷(文科)(解析版) 题型:解答题
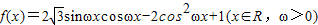 的周期为π.
的周期为π. 时,若f(θ)=1,求θ值.
时,若f(θ)=1,求θ值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省泰州市姜堰市蒋垛中学高三数学综合练习4(文科)(解析版) 题型:解答题
 的周期为T,在一个周期内的图象如图所示,则φ= .
的周期为T,在一个周期内的图象如图所示,则φ= .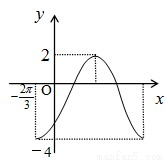
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试理科数学(福建卷解析版) 题型:解答题
已知函数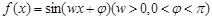 的周期为
的周期为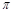 ,图象的一个对称中心为
,图象的一个对称中心为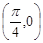 ,将函数
,将函数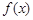 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个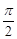 单位长度后得到函数
单位长度后得到函数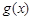 的图象。
的图象。
(Ⅰ)求函数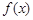 与
与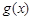 的解析式
的解析式
(Ⅱ)是否存在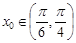 ,使得
,使得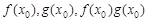 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定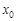 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;
(Ⅲ)求实数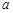 与正整数
与正整数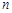 ,使得
,使得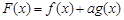 在
在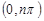 内恰有2013个零点
内恰有2013个零点
查看答案和解析>>
科目:高中数学 来源:浙江省富阳市2009-2010学年度高一数学期中试卷 题型:选择题
已知函数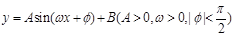 的周期为T,在一个周期内的图像如图所示,则正确的结论是( )
的周期为T,在一个周期内的图像如图所示,则正确的结论是( )
A.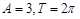 B.
B.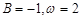
C.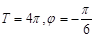 D.
D.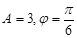
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com