
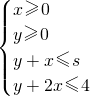 下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是 ________.
下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是 ________. 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,

科目:高中数学 来源:新课标高三数学基本不等式、简单的线性规划问题专项训练(河北) 题型:填空题
在约束条件下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是_________
查看答案和解析>>
科目:高中数学 来源:吉林一中2009-2010学年上学期期末高二(数学)试题 题型:选择题
在约束条件 下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
A. B.[7,8] C.[6,8] D.[7,15]
B.[7,8] C.[6,8] D.[7,15]
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省武汉市华中师大一附中高二(上)期中数学试卷(理科)(解析版) 题型:选择题
 下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com