
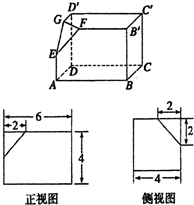
 如图为一长方体截去一个角后所得多面体的直观图以及它的正视图和侧视图.
如图为一长方体截去一个角后所得多面体的直观图以及它的正视图和侧视图.
| 1 |
| 3 |
| 1 |
| 2 |
| 284 |
| 3 |
| 284 |
| 3 |


科目:高中数学 来源: 题型:
 如图所示,在三棱柱A1B1C1-ABC中,AA1⊥底面ABC,AC⊥BC.AC=BC=CC1=2.
如图所示,在三棱柱A1B1C1-ABC中,AA1⊥底面ABC,AC⊥BC.AC=BC=CC1=2.查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示, 在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
,![]()
![]() .
.
(1)若点![]() 分别为棱
分别为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2) 请根据下列要求设计切割和拼接方法:要求用平行于三棱柱![]() 的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).
的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,并写出拼接后的长方体的表面积(不必写出计算过程).

查看答案和解析>>
科目:高中数学 来源:2014届河北省高一下学期期中数学试卷(解析版) 题型:填空题
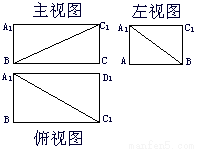
如图是一个长方体ABCD-A1B1C1D1截去一
个角后的多面体的三视图,在这个多面体中,
AB=4,BC=6,CC1=3.则这个多面体的体积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示, 在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
,![]()
![]() .
.
(1)若点![]() 分别为棱
分别为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2) 请根据下列要求设计切割和拼接方法:要求用平行于三棱柱![]() 的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,
的某一条侧棱的平面去截此三棱柱,切开后的两个几何体再拼接成一个长方体. 简单地写出一种切割和拼接方法,
并写出拼接后的长方体的表面积(不必计算过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com