Question

【题目】【2016高考浙江文数】如图，设抛物线的焦点为F，抛物线上的点A到y轴的距离等于|AF|-1.

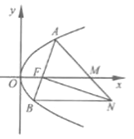
（I）求p的值；

（II）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x

轴交于点M.求M的横坐标的取值范围.

Answer 1

【答案】（I）；（II）.

【解析】

试题分析：（I）由抛物线的定义可得的值；（II）设点的坐标和直线的方程，通过联立方程组可得点的坐标，进而可得点的坐标，再利用，，三点共线可得用含有的式子表示，进而可得的横坐标的取值范围.

试题解析：(Ⅰ)由题意可得抛物线上点A到焦点F的距离等于点A到直线x=-1的距离.

由抛物线的定义得，即p=2.

(Ⅱ)由(Ⅰ)得抛物线的方程为，可设.

因为AF不垂直于y轴，可设直线AF:x=sy+1, ,由 消去x得

，故，所以.

又直线AB的斜率为，故直线FN的斜率为，

从而的直线FN:，直线BN:，

所以，

设M(m,0),由A,M,N三点共线得： ，

于是，经检验，m<0或m>2满足题意.

综上，点M的横坐标的取值范围是.