

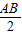 的正方形面积减去半径为
的正方形面积减去半径为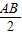 的四分之一圆的面积得到.
的四分之一圆的面积得到.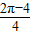 =
=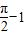 ,
,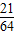


科目:高中数学 来源: 题型:
 如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域.
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域.查看答案和解析>>
科目:高中数学 来源:0117 期中题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域.
(1)若向该正方形内随机投一点,求该点落在阴影区域的概率?
(2)给正方形ABCD的四个顶点都作上一个标记,现有四种标记可供选择,记“任一线段上的两个顶点标记都不同”为事件A,求事件A发生的概率
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com