已知定圆Q:x2+y2-2x-15=0,动圆M和已知圆内切,且过点P(-1,0),
(1)求圆心M的轨迹及其方程;
(2)试确定m的范围,使得所求方程的曲线C上有两个不同的点关于直线l:y=4x+m对称.
分析:(1)由圆Q:x2+y2-2x-15=0,我们易判断出圆Q的圆心为(1,0),半径为4,又由动圆M和已知圆内切,且过点P(-1,0),根据椭圆的定义,易得M的轨迹是以P,Q为焦点的椭圆,进而求出圆心M的轨迹及其方程;
(2)若所求方程的曲线C上有两个不同的点关于直线l:y=4x+m对称,则P、Q到直线l的距离相等,即线段PQ的中点M在直线l上,不妨另直线PQ与椭圆一定有两个交点,由一元二次方程根与系数的关系,构造关于m,n的方程组,即可得到满足条件的m的范围.
解答:解 (1)已知圆可化为(x-1)
2+y
2=16,设动圆圆心M(x,y),则|MP|为半径,又圆M和圆Q内切,即|MP|+|MQ|=4,故M的轨迹是以P,Q为焦点的椭圆,且PQ中心为原点,故动圆圆心M的轨迹方程是
+=1(2)假设具有对称关系的两点所在直线l′的方程为
y=-x+n,代入椭圆方程中有
3x2+4(-x+n)2-12=0,即13x
2-8nx+16n
2-48=0.
若要椭圆上关于直线l对称得不同两点存在,则需l′与椭圆相交,且两交点P、Q到直线l的距离相等,即线段PQ的中点M在直线l上,
故△=64n
2-4×13×(16n
2-48)>0,∴
-<n<.
设P(x
1,y
1),Q(x
2,y
2),
则
x1+x2=,
y1+y2=-(x1+x2)+2n=n,∴
=4×+m,
故
m=-,∴
n=-,
∴
-<-<,
即
-<m<.
点评:本题考查的知识点是圆与圆的位置关系及其判定,关于点、直线对称的圆的方程,其中熟练掌握圆、椭圆的定义及性质是解答本题的关键.



 互动英语系列答案
互动英语系列答案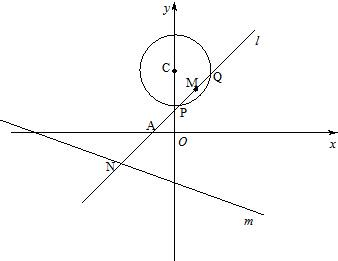 如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.
如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.