

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
| | 不患肺癌 | 患肺癌 | 总计 |
| 不吸烟 | 7775 | 42 | 7817 |
| 吸烟 | 2099 | 49 | 2148 |
| 总计 | 9874 | 91 | 9965 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
| [12.45,12.95) | 2 | 0.2 |
| [12.95,13.45) | 0.3 | |
| [13.45,13.95) | 4 | |
| [13.95,14.45) | 1 | 0.1 |
| 合 计 | 10 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.6 | B.36 | C.60 | D.120 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.28 | B.38 | C.48 | D.58 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 150 | 500 | 250 | 75 | 25 |
| 分组(平方米) | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 | 100.5~120.5 | 120.5~140.5 | 140.5~160.5 | 合计 |
| 百分比 | 4% | 12% | 36% | 20% | 4% | 1.00 |
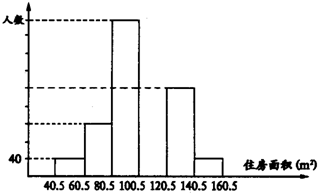
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com