练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-1-18所示,长方体AC1中,底面ABCD为边长为2的正方形,高AA1为1,M、N分别是边C1D1与A1D1的中点.

    图2-1-18

    (1)求证:四边形MNAC是等腰梯形;

    (2)求梯形MNAC的面积.

    思路分析:(1)要证明一个四边形是等腰梯形,应证明①四边形是平面图形;②有一组对边平行;③另一组对边不相等.

    (2)只需利用(1)的结论,并利用梯形的面积公式,即可得出问题的解答.

    (1)证明:连结A1C1,则MN是△A1C1D1的中位线,

    于是MNA1C1.

    又A1C1AC,

    ∴MNAC.

    ∴M、N、A、C共面,且四边形MNAC为梯形.

    ∵Rt△AA1N≌Rt△CC1M,

    ∴AN1=CM.

    ∴梯形MNAC为等腰梯形.

    (2)解:AN2=A1A2+A1N2=1+1=2,AC=,MN=,

    梯形的高为h=,

    ∴S梯形ACMN= (AC+MN)×h=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•河南模拟）某高中社团进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的为“时尚族”，否则称为“非时尚族”．通过调查分别得到如图1
    所示统计表和如图2所示各年龄段人数频率分布直方图：


    请完成以下问题：
    （1）补全频率直方图，并求n，a，p的值
    （2）从[40，45）岁和[45，50）岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁得人数为X，求X的分布列和数学期望E（X）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的图象如图1-2-18所示,则f(x)的解析式是_________.

             图1-2-18

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省豫南九校高三第四次联考理科数学 题型：解答题

    （本小题满分12分）

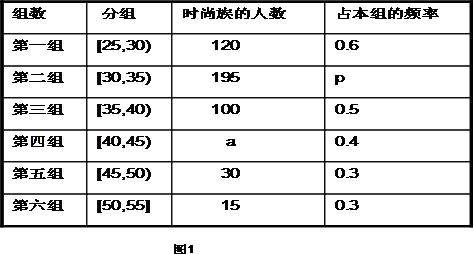
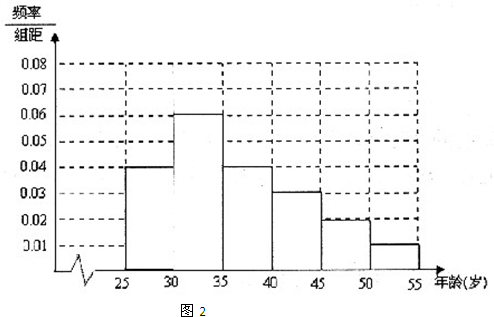
        某高中社团进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”。通过调查分别得到如图1所示统计表如图2所示各年龄段人数频率分布直方图：

    请完成下列问题：

    （1）补全频率分布直方图，并求的值；

    （2）从岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛，其中选取3人作为领队，求选取的3名领队年龄在岁的人数为X，求X的分布列和期望E（X）。

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省海珠区高三第一次综合测试数学理卷 题型：选择题

    直角梯形如图1,动点P从点B出发,由沿边运动,设点P运动的路程为,的面积为.如果函数的图象如图2所示,则的面积为

    A．10         B．32          C．18              D．16

     

     

     

    查看答案和解析>>

    同步练习册答案