
已知抛物线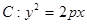 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与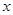 轴的焦点,过P的直线
轴的焦点,过P的直线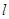 与抛物线C交于A、B两点.
与抛物线C交于A、B两点.
(1)当线段AB的中点在直线 上时,求直线
上时,求直线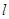 的方程;
的方程;
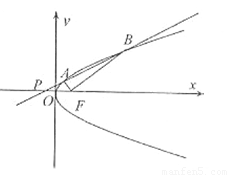
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积.
(1)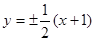 . (2)
. (2)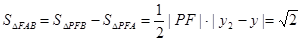 .
.
【解析】
试题分析:(1)首先确定抛物线方程为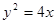 ,将直线
,将直线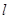 的方程为
的方程为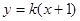 ,(依题意
,(依题意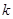 存在,且
存在,且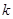 ≠0)与抛物线方程联立,消去
≠0)与抛物线方程联立,消去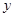 得应用中点坐标公式AB中点的横坐标为
得应用中点坐标公式AB中点的横坐标为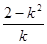 ,进一步求得直线的斜率,从而可得直线方程.应注意直线斜率的存在性.
,进一步求得直线的斜率,从而可得直线方程.应注意直线斜率的存在性.
(2)根据中点坐标公式确定得到,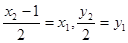 再利用A、B为抛物线上点,得得到方程组求得
再利用A、B为抛物线上点,得得到方程组求得
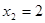 ,
,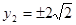 ,计算得到△FAB的面积
,计算得到△FAB的面积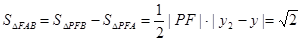 .注意结合图形分析,通过确定点的坐标,得到三角形的高线长.
.注意结合图形分析,通过确定点的坐标,得到三角形的高线长.
试题解析:(1)因为抛物线的准线为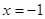 ,所以
,所以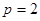 ,
,
抛物线方程为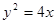 2分
2分
设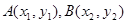 ,直线
,直线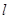 的方程为
的方程为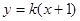 ,(依题意
,(依题意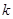 存在,且
存在,且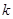 ≠0)与抛物线方程联立,消去
≠0)与抛物线方程联立,消去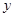 得
得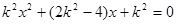 (*)
(*)
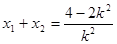 ,
, 4分
4分
所以AB中点的横坐标为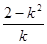 ,即
,即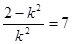 ,所以
,所以 6分
6分
(此时(*)式判别式大于零)
所以直线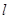 的方程为
的方程为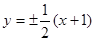 7分
7分
(2)因为A为线段PB中点,所以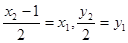 8分
8分
由A、B为抛物线上点,得 ,
,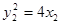 10分
10分
解得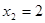 ,
,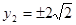 11分
11分
当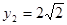 时,
时,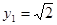 ;当
;当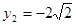 时,
时,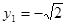 12分
12分
所以△FAB的面积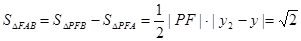 14分
14分
考点:抛物线标准方程,直线与抛物线的位置关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知抛物线![]() ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与![]() 轴的焦点,过P的直线
轴的焦点,过P的直线![]() 与抛物线C交于A、B两点。
与抛物线C交于A、B两点。
(1)当线段AB的中点在直线![]() 上时,求直线
上时,求直线![]() 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积。
查看答案和解析>>
科目:高中数学 来源:2014届广西柳州铁路一中高二上学期第一次月考数学试卷(解析版) 题型:选择题
已知抛物线 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线 和
和 轴的距离之和的最小值
轴的距离之和的最小值
是( )
A. B.
B. C.2 D.
C.2 D.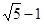
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com