
(2006
福建,18)如下图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2, .
.
(1)
求证:AO⊥平面BCD;(2)
求异面直线AB与CD所成角的大小;(3)
求点E到平面ACD的距离.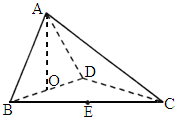
|
解析: (1)连结OC.∵ BO=DO,AB=AD,∴AO⊥BD.∵ BO=DO,BC=CD,∴CO⊥BD.
在△ AOC中,由已知可得AO=1,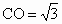 ,而AC=2, ,而AC=2,
∴ 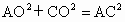 , ,
∴∠ AOC=90°,即AO⊥OC.∵ BD∩OC=O,∴ AO⊥平面BCD.(2) 取AC的中点M,连结OM、ME、OE,由E为BC的中点知ME∥AB,OE∥DC.∴直线 OE与EM所成的锐角就是异面直线AB与CD所成的角.在△ OME中,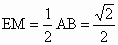 , ,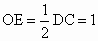 , ,
∵ OM是直角△AOC斜边上的中线,∴ 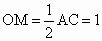 ,∴ ,∴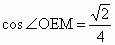 , ,
∴异面直线 AB与CD所成角的大小为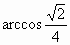 . .
(3) 设点E到平面ACD的距离为h.∵ 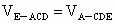 , ,
∴ 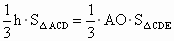 . .
在△ ACD中,CA=CD=2,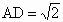 . .
∴ 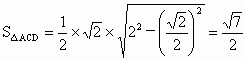 . .
而 AO=1,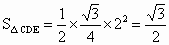 , ,
∴ 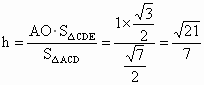 . .
∴点 E到平面ACD的距离为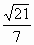 . . |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com