设a=lnz+ln[x(yz)-1+1],b=lny+ln[(xyz)-1+1],记a,b中最大数为M,则M的最小值为 .
【答案】
分析:由题意,M=max{a,b}所以M≥a,M≥b上述两不等式相加得 2M≥(a+b),又 a+b=lnz+ln[x(yz)
-1+1]+lny+ln[(xyz)
-1+1]=
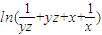
,利用基本不等式可求M的最小值.
解答:解:由题意,M=max{a,b}
所以M≥a,M≥b
上述两不等式相加
得 2M≥(a+b)
且 a+b=lnz+ln[x(yz)
-1+1]+lny+ln[(xyz)
-1+1]
=
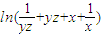
用基本不等式 得上式≥ln(2+2)=ln4
所以2M≥ln4 M≥ln2
所以M的最小值是ln2
故答案为ln2
点评:本题以等式为载体,考查基本不等式的运用,有一定的难度.
