Question

在一次“知识竞赛”活动中，有A₁，A₂，B，C四道题，其中A₁，A₂为难度相同的容易题，B为中档题，C为较难题．现甲、乙两位同学均需从四道题目中随机抽取一题作答．
（Ⅰ）求甲、乙两位同学所选的题目难度相同的概率；
（Ⅱ）求甲所选题目的难度大于乙所选题目的难度的概率．

Answer 1

【答案】分析：（Ⅰ）先列举出所有可能的结果有16个，找出其中事件“甲、乙两位同学所选的题目难度相同”包含的基本事件有6个，从而求得甲、乙两位同学所选的题目难度相同的概率．
（Ⅱ）在所有的基本事件中找出事件“甲所选题目的难度大于乙所选题目的难度”包含的基本事件的个数，可得甲所选题目的难度大于乙所选题目的难度的概率．
解答：解：由题意可知，甲、乙两位同学分别从四道题中随机抽取一题，所有可能的结果有16个，
它们是：（A₁，A₁），（A₁，A₂），（A₁，B），（A₁，C），（A₂，A₁），（A₂，A₂），（A₂，B），
（A₂，C），（B，A₁），（B，A₂），（B，B），（B，C），（C，A₁），（C，A₂），（C，B），（C，C）．
（Ⅰ）用M表示事件“甲、乙两位同学所选的题目难度相同”，
则M包含的基本事件有：（A₁，A₁），（A₁，A₂），（A₂，A₁），（A₂，A₂），（B，B），（C，C），共有6个．
所以．
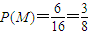
（Ⅱ）用N表示事件“甲所选题目的难度大于乙所选题目的难度”，
则N包含的基本事件有：（B，A₁），（B，A₂），（C，A₁），（C，A₂，），（C，B），共有5个．
所以．
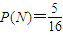
点评：本题考查古典概型问题，可以列举出试验发生包含的事件和满足条件的事件，列举法，是解决古典概型问题的一种重要的解题方法，属于基础题．
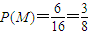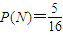