
设a,b为实数,关于x的方程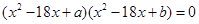 的4个实数根构成以d为公差的等差数列,若
的4个实数根构成以d为公差的等差数列,若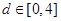 ,则
,则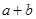 的取值范围是 .
的取值范围是 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
已知定义在R上的偶函数满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;
②x=-4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]上单调递增;
④若方程f(x)=m在[-6,-2]上的两根为x1,x2则x1+x2=-8.以上命题中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
(2014·黄冈模拟)f(x)是定义在R上的偶函数,当x<0时,有f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
[2014·合肥模拟]f(x)是定义在(0,+∞)上的单调递增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com