Question

18．在如图所示的正方体中．
（1）指出哪些棱与BB₁是异面直线，哪些棱与对角线BD₁是异面直线．
（2）分别求出直线DD₁与BC₁、A₁D₁及DC₁所成的角度．

Answer 1

分析 （1）结合正方体的结构特征和异面直线的概念能求出结果．
（2）由DD₁∥CC₁，得∠BC₁C是直线DD₁与BC₁所成的角的大小，由此能求出直线DD₁与BC₁所成角；由A₁D₁⊥平面DCC₁D₁，能求出A₁D₁及DC₁所成的角的大小．

解答 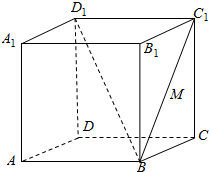解：（1）在正方体ABCD-A₁B₁C₁D₁中，
与BB₁是异面直线的棱有：AD、A₁D₁、CD、C₁D₁；
与对角线BD₁是异面直线的棱有：AA₁、CC₁、AD、B₁C₁、CD、A₁B₁．
（2）∵DD₁∥CC₁，∴∠BC₁C是直线DD₁与BC₁所成的角，
∵在正方体ABCD-A₁B₁C₁D₁中，BC=CC₁，BC⊥CC₁，
∴∠BC₁C=45°，
∴直线DD₁与BC₁所成角为45°．
∵在正方体ABCD-A₁B₁C₁D₁中，A₁D₁⊥平面DCC₁D₁，
DC₁?平面DCC₁D₁，
∴A₁D₁⊥DC₁，
∴A₁D₁及DC₁所成的角为90°．

点评 本题考查异面直线的判断和导面直线所成角的大小的求法，是基础题，解题时要认真审题，注意正方体的结构特征和异面直线的概念的合理运用．