分析:(1)在△F
1PF
2中,MO为中位线,根据三角形的中位线定理再结合椭圆的定义即可得出答案;
(2)先利用椭圆的定义得到:|PF
1|+|PF
2|=10,再在△PF
1F
2中利用余弦定理得出cos 60°=
| |PF1|2+|PF2|2-|F1F2|2 |
| 2|PF1||PF2| |
,两者结合即可求得|PF
1|•|PF
2|;
(3)先设点P(x
0,y
0),根据椭圆的性质,易知F
1(-3,0),F
2(3,0),写出向量的坐标再结合向量垂直的条件得出关于P点坐标的方程组,由此方程组无解,故这样的点P不存在.
解答: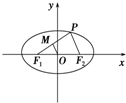
证明:(1)在△F
1PF
2中,MO为中位线,
∴|MO|=
=
=a-
=5-
|PF
1|….(3分)
(2)解:∵|PF
1|+|PF
2|=10,
∴|PF
1|
2+|PF
2|
2=100-2|PF
1|•|PF
2|,
在△PF
1F
2中,cos 60°=
| |PF1|2+|PF2|2-|F1F2|2 |
| 2|PF1||PF2| |
,
∴|PF
1|•|PF
2|=100-2|PF
1|•|PF
2|-36,
∴|PF
1|•|PF
2|=
.…(8分)
(3)解:设点P(x
0,y
0),则
+=1.①
易知F
1(-3,0),F
2(3,0),故
=(-3-x
0,-y
0),
=(3-x
0,-y
0),
∵
•=0,
∴x
-9+y
=0,②
由①②组成方程组,此方程组无解,故这样的点P不存在. …(12分)
点评:本小题主要考查椭圆的标准方程、椭圆的简单性质、解三角形等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

 证明:(1)在△F1PF2中,MO为中位线,
证明:(1)在△F1PF2中,MO为中位线,

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案