
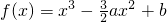 ,a,b为实数,x∈R,a∈R.
,a,b为实数,x∈R,a∈R.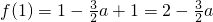 ,
,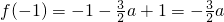 ,∴f(-1)<f(1).
,∴f(-1)<f(1).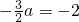 ,得
,得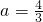 .故
.故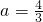 ,b=1为所求.…(6分)
,b=1为所求.…(6分)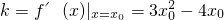 ,
,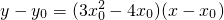 .…(10分)
.…(10分)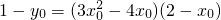 ,
,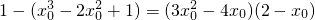 ,∴
,∴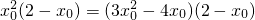 ,
,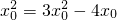 ,即2x0(x0-2)=0,∴x0=0.∴切线l的方程为y=1.
,即2x0(x0-2)=0,∴x0=0.∴切线l的方程为y=1.| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| F′(x) | + | 0 |  | 0 | + |
| F(x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
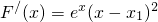 ,此时无极值.…(16分)
,此时无极值.…(16分)

科目:高中数学 来源:2015届山东省济宁市高一3月质量检测数学试卷(解析版) 题型:解答题
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3,"
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3,"
x2=4.
(1)求函数f(x)的解析式;
(2)设 ,解关于x的不等式;
,解关于x的不等式; .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010年上海市华东师大二附中高三数学综合练习试卷(07)(解析版) 题型:解答题
 (a,b为实常数),若f(x)的值域为[0,+∞),则常数a,b应满足的条件 .
(a,b为实常数),若f(x)的值域为[0,+∞),则常数a,b应满足的条件 .查看答案和解析>>
科目:高中数学 来源:2006年上海市奉贤区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 (a,b为实常数),若f(x)的值域为[0,+∞),则常数a,b应满足的条件 .
(a,b为实常数),若f(x)的值域为[0,+∞),则常数a,b应满足的条件 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com