Question

14．如图，在正方体ABCD-A₁B₁C₁D₁中，M为CC₁的中点．
（1）求证：BD⊥A₁M；
（2）求证：平面A₁BD⊥平面MBD．

Answer 1

分析 （1）设正方体ABCD-A₁B₁C₁D₁的棱长为2，以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能证明BD⊥A₁M．
（2）求出平面A₁BD的法向量和设平面MBD的法向量，由两平面的法向量的数量积为0，能证明平面A₁BD⊥平面MBD．

解答 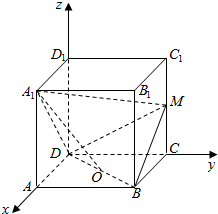（1）证明：设正方体ABCD-A₁B₁C₁D₁的棱长为2，
以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
则B（2，2，0），D（0，0，0），A₁（2，0，2），M（0，2，1），
$\overrightarrow{DB}$=（2，2，0），$\overrightarrow{{A}_{1}M}$=（-2，2，-1），
∴$\overrightarrow{DB}•\overrightarrow{{A}_{1}M}$=-4+4+0=0，
∴BD⊥A₁M．
（2）$\overrightarrow{D{A}_{1}}$=（2，0，2），$\overrightarrow{DB}$=（2，2，0），$\overrightarrow{DM}$=（0，2，1），
设平面A₁BD的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=2x+2z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=2x+2y=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，-1，-1），
设平面MBD的法向量$\overrightarrow{m}$=（a，b，c），
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DB}=2a+2b=0}\\{\overrightarrow{m}•\overrightarrow{DM}=2b+c=0}\end{array}\right.$，取a=1，得$\overrightarrow{m}$=（1，-1，2）
∵$\overrightarrow{n}•\overrightarrow{m}$=1+1-2=0，
∴平面A₁BD⊥平面MBD．

点评 本题考查异面直线垂直的证明，考查两平面垂直的证明，是中档题，解题时要认真审题，注意向量法的合理运用．