方程log2(2-2x)+x+99=0的两个解的和是________.
-99
分析:设方程log
2(2-2
x)+x+99=0的两个解为x
1,x
2,令t=2
x,则x=log
2t,将方程转化为一元二次方程,利用韦达定理可求得结论.
解答:设方程log
2(2-2
x)+x+99=0的两个解为x
1,x
2,
令t=2
x,∴x=log
2t
∵log
2(2-2
x)+x+99=0
∴log
2(2-t)+log
2t+99=0
∴log
2[(2-t)t]=-99
∴(2-t)t=2
-99∴t
2-2t+2
-99=0
设方程两根为t
1,t
2,
∴t
1t
2=2
-99∴
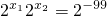
∴x
1+x
2=-99
故答案为:-99
点评:本题考查方程根的研究,考查转化思想,考查韦达定理的运用,属于基础题.
