Question

已知|a.|=3,b=(2,3),试分别解答下面两个问题:

(1)若a.⊥b,求a;

(2)若a∥b,求a.

Answer 1

活动:对平面中的两向量a=(x₁,y₁)与b=(x₂,y₂),要让学生在应用中深刻领悟其本质属性,向量垂直的坐标表示x₁x₂+y₁y₂=0与向量共线的坐标表示x₁y₂-x₂y₁=0很容易混淆,应仔细比较并熟记,当难以区分时,要从意义上鉴别,两向量垂直是a·b=0,而共线是方向相同或相反.教师可多加强反例练习,多给出这两种类型的同式变形训练.

解:(1)设a=(x,y),由|a.|=3且a⊥b,

得

解得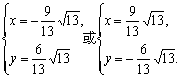

∴a=(a=

(2)设a=(x,y),由|a|=3且a∥b,得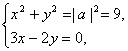

解得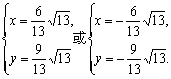

∴aa

点评:本题主要考查学生对公式的掌握情况,学生能熟练运用两向量的坐标运算来判断垂直或者共线,也能熟练地进行公式的逆用,利用已知关系来求向量的坐标.