
已知函数 .
.
(1)求证: 时,
时, 恒成立;
恒成立;
(2)当 时,求
时,求 的单调区间.
的单调区间.
(1)详见试题解析;(2)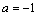 时,
时,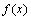 的单调递增区间为
的单调递增区间为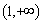 ,单调递减区间为
,单调递减区间为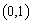 ;
;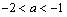 时,
时,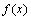 的单调递增区间为
的单调递增区间为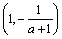 ,单调递减区间为
,单调递减区间为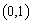 和
和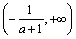 ;
;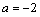 时,
时,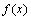 的单调递减区间为
的单调递减区间为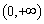 ,无单调增区间.
,无单调增区间.
【解析】
试题分析:(1)当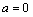 时,
时,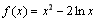 ,根据求函数极值的一般步骤,先求函数
,根据求函数极值的一般步骤,先求函数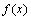 的定义域,再求导数,解
的定义域,再求导数,解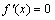 的方程,得可能的极值点,进一步得函数
的方程,得可能的极值点,进一步得函数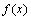 的单调性,最后得
的单调性,最后得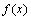 的最小值,从而证得
的最小值,从而证得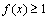 恒成立;(2)当
恒成立;(2)当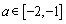 时,先求
时,先求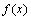 的导数:
的导数: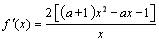 ,根据
,根据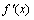 表达式的结构特征,分子为
表达式的结构特征,分子为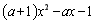 ,故只需分
,故只需分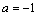 ,
,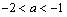 ,
,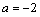 几种情况,分别求函数
几种情况,分别求函数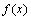 的单调区间.
的单调区间.
试题解析:(1)当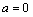 时,
时,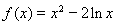 ,
,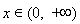 ,
,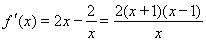 ,令
,令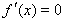 ,解得:
,解得: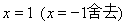 .当
.当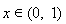 时,
时,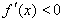 ,
,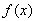 在
在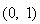 上单调递减; 当
上单调递减; 当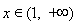 时,
时,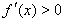 ,
,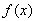 在
在 上单调递增,∴
上单调递增,∴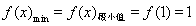 .
.
所以,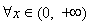 ,
, 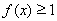 . 5分
. 5分
(2)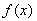 的定义域为
的定义域为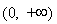 ,
,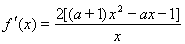 .
.
①当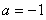 时,
时,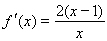 ,此时
,此时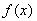 在区间
在区间 上单调递增,在
上单调递增,在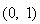 上单调递减;
上单调递减;
②当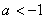 时,
时,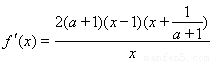 .令
.令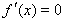 ,解得:
,解得: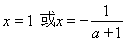 .
.
ⅰ)当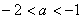 时,
时,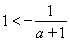 ,令
,令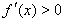 ,解得:
,解得: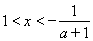 .令
.令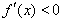 ,解得:
,解得: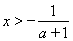 或
或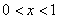 ,此时
,此时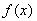 在区间
在区间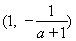 上单调递增,在
上单调递增,在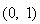 和
和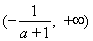 上单调递减.
上单调递减.
ⅱ)当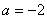 时,
时,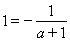 ,此时
,此时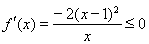 ,
,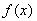 在区间
在区间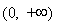 上单调递减.
上单调递减.
综上,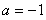 时,
时,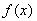 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为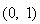 ;
;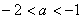 时,
时,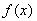 的单调递增区间为
的单调递增区间为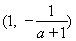 ,单调递减区间为
,单调递减区间为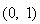 和
和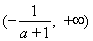 ;
;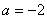 时,
时,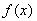 的单调递减区间为
的单调递减区间为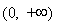 ,无单调增区间. 13分
,无单调增区间. 13分
考点:1.利用导数证明不等式;2.利用导数讨论函数的单调性.


科目:高中数学 来源:2012-2013学年宁夏高三第五次月考理科数学试卷(解析版) 题型:解答题
(本小题满分l0分)选修4—5:不等式选讲
已知函数 .
.
(1)求证: ;
;
(2)解不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西吉安宁冈中学高三下学期第一次月考文科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求证函数 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
)
(2)当 时,若关于
时,若关于 的不等式
的不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省鹰潭市高三第二次模拟考试理科数学卷 题型:解答题
已知函数 .
.
(1)求证函数 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
)
(2)当 时,若关于
时,若关于 的不等式
的不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com