
| A. | an=2n-1 | B. | ${a_n}=\left\{\begin{array}{l}2,n=1\\ 2n-1,n>1\end{array}\right.$ | ||
| C. | an=2n+1 | D. | ${a_n}=\left\{\begin{array}{l}2,n=1\\ 2n+1,n>1\end{array}\right.$ |
分析 根据关系式:an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,进行求解,最后验证n=1时是否成立.
解答 解:由题意知,当n=1时,a1=s1=1+1=2,
当n≥2时,an=sn-sn-1=(n2+1)-[(n-1)2+1)]=2n-1,
经验证当n=1时不符合上式,
∴${a_n}=\left\{\begin{array}{l}2,n=1\\ 2n-1,n>1\end{array}\right.$.
故选:C.
点评 本题考查了数列通项公式和前n项和公式之间的关系式,即an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,注意验证n=1时是否成立,这是容易忽视的地方.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<c<a | B. | a<b<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
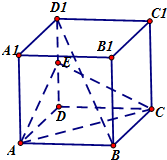 如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 14 | 18 | 19 | 20 | 23 | 25 | 28 |
| A. | 一次函数模型 | B. | 二次函数模型 | C. | 指数函数模型 | D. | 对数函数模型 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com