
| A. | ① | B. | ② | C. | ③ | D. | ①③ |
分析 直接利用新定义,逐一判断选项即可.
解答 解:函数f(x)的定义域为R,若?常数c>0,对?x∈R,都有f(x)+c≥f(x+c),
则称函数f(x)具有性质P,给定下列三个函数:
对于①f(x)=$\frac{1}{2}$x+1;f(x)+c=$\frac{1}{2}$x+1+c>$\frac{1}{2}$x+1+$\frac{c}{2}$=f(x+c),满足新定义,所以①正确;
对于②f(x)=x2;f(x)+c=x2+c;
f(x+c)=(x+c)2=x2+2cx+c2,对?x∈R,1≥2x+c,不恒成立,所以②不正确;
对于③f(x)=2x,f(x)+c=2x+c;
f(x+c)=2x+c=2c2x,如果f(x)+c≥f(x+c),可得2x+c≥2c2x,即$\frac{c}{{2}^{c}-1}≥{2}^{x}$,
此式对于?x∈R不恒成立,所以③不满足新定义.
故选:A.
点评 本题考查新定义的应用,函数与方程的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33 | B. | 43 | C. | 53 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若Χ2的观测值为6.64,而P(Χ2≥6.64)=0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 | |
| B. | 从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 | |
| C. | 若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推判出现错误 | |
| D. | 以上三种说法都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
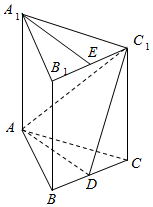 如图,在正三棱柱ABC-A1B1C1中,点D、E分别为BC、B1C1的中点,且AB=AA1=2.
如图,在正三棱柱ABC-A1B1C1中,点D、E分别为BC、B1C1的中点,且AB=AA1=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com