
 =(3,4),
=(3,4), =(4,3),求x,y的值使(x
=(4,3),求x,y的值使(x +y
+y )
)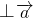 ,且|x
,且|x +y
+y |=1.
|=1. =(3,4),
=(3,4), =(4,3),∴(x
=(4,3),∴(x +y
+y )=(3x+4y,4x+3y),
)=(3x+4y,4x+3y), +y
+y )
)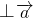 ,∴(x
,∴(x +y
+y )•
)• =3(3x+4y )+4(4x+3y)=0,即 25x+24y=0 ①.
=3(3x+4y )+4(4x+3y)=0,即 25x+24y=0 ①. +y
+y |=1,可得 (3x+4y)2+(4x+3y)2=1,
|=1,可得 (3x+4y)2+(4x+3y)2=1, ,
, 和
和 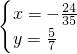 .
. +y
+y )
)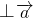 ,可得(x
,可得(x +y
+y )•
)• =0,即 25x+24y=0 ①.再由|x
=0,即 25x+24y=0 ①.再由|x +y
+y |=1,可得 x(25x+24y)+24xy+25y2=1 ②.由①②可求得x,y的值.
|=1,可得 x(25x+24y)+24xy+25y2=1 ②.由①②可求得x,y的值.

科目:高中数学 来源: 题型:
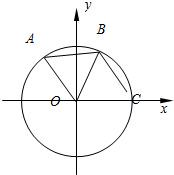 如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.
如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com