
 是R上奇函数.
是R上奇函数.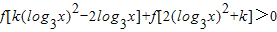 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. ,令log3x=t,则(k+2)t2-2t+k>0对一切实数t恒成立.由此能求出实数k的取值范围.
,令log3x=t,则(k+2)t2-2t+k>0对一切实数t恒成立.由此能求出实数k的取值范围. 是R上奇函数,
是R上奇函数,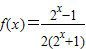 经检验确为奇函数,
经检验确为奇函数,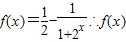 在R上单调递增,
在R上单调递增, ,
, ,
, .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com