分析:(1)根据
b1=,求得
a1=-,从而
b2=a2=;
(2)将
bn+1=1+代入得到:
an+1====-2an-1即可证得:a
n+1+2a
n+1=0;
(3)由(2)所得结论变形得到:
an+1+=-2 (an+)从而得出数列
{an+}是以-2为首项,公比为-2的等比数列,最后利用等比数列的通项公式即可求出数列{a
n}的通项公式;
(4)由(3)得出数列{a
n}的通项公式写出数列bn,下面对n进行奇偶数讨论:①当n为偶数时②当n为奇数时,分别利用等比数列的前n项结合不等式的放缩即可得到证明.
解答:解:(1)∵
b1=∴
a1=-∴
b2=a2=…(3分)
(2)证明:∵
an+1====-2an-1∴a
n+1+2a
n+1=0…(5分)
(3)∵a
n+1=-2a
n-1∴
an+1+=-2 (an+)…(6分)
又
a1+=-2 ≠0∴数列
{an+}是以-2为首项,公比为-2的等比数列…(7分)
∴
an+=(-2)n∴
an=(-2)n-…(8分)
(4)
bn=+2=+2∴
(-1)nbn=2•(-1)n+当n为奇数时(-1)
nb
n+(-1)
n+1b
n+1=
+=
<=+,
①当n为偶数时,(-1)b
1+(-1)
2b
2+…+(-1)
nb
n<++…++<=1,
②当n为奇数时,(-1)b
1+(-1)
2b
2+…+(-1)
nb
n<++…++-2+<-2+=
-1<1…(11分)
综上所述:(-1)b
1+(-1)
2b
2+…+(-1)
nb
n<1…(12分)
点评:本小题主要考查数列递推式、数列与不等式的综合、不等式的性质等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 ,
, ,数列{an}满足:
,数列{an}满足: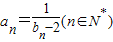 .
.