
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 3 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
| 2 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 运动 | 非运动 | 总计 | |||||||
| 男 |
|
|
| ||||||
| 女 |
|
|
| ||||||
| 总计 |
|
|
n |
n(
| ||||||||
|
| n |
| 36 |
| n |
| 36 |
| n |
| 5 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
在对人们休闲方式的一次调查中,根据数据建立如下的2×2列联表:
(参考数据:P(x2≥3.841)≈0.05,P(x2≥6.635)≈0.01) |
查看答案和解析>>
科目:高中数学 来源:2013届山东省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)在犯错误的概率不超过0.10的前提下,认为休闲方式与性别是否有关?
参考数据:独立性检验临界值表
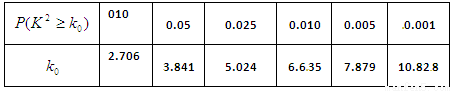
参考公式:独立性检验随机变量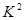 值的计算公式:
值的计算公式: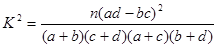 (其中
(其中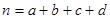 )
)
查看答案和解析>>
科目:高中数学 来源:2010年福建省厦门市高二下学期质量检测(理科)数学卷 题型:解答题
(本小题满分 12分
12分 )
)
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。
 (I)根据以上数据建立一个2×2的列联表:
(I)根据以上数据建立一个2×2的列联表:
|
休闲方式 性别 |
看电视 |
运动 |
总计 |
|
女性 |
|
|
|
|
男性 |
|
|
|
|
总计 |
|
|
|
(II)休闲方式与性别是否有关?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市安溪一中、惠安一中、养正中学联考高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,女性占总调查人数的
,女性占总调查人数的 ,其中男性有一半的休闲方式是运动;而女性只有
,其中男性有一半的休闲方式是运动;而女性只有 的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?
的休闲方式是运动,经过调查人员的计算:在犯错误的概率不超过0.05的前提下,认为休闲方式与性别有关,那么被调查的人中最少有多少人的休闲方式是运动?| P(K2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com