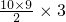练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数列{an}中，若a1=-4，an+1=an+3，则|a1|+|a2|+…+|a10|=


    1. A.
      23
    2. B.
      95
    3. C.
      100
    4. D.
      105
    D
    分析：先求数列的通项公式，再根据数列的通项公式弄清数列从第几项起符号发生改变，然后代入|a1|+|a2|+…+|a10|求解即可．
    解答：∵a1=-4，an+1=an+3，∴an+1-an=3，
    即数列{an}为-4为首项，3为公差的等差数列，
    故an=-4+3（n-1）=3n-7，由3n-7＞0解得n＞，
    ∴数列{an}的前2项为负数，从第3项起为正数，
    ∴|a1|+|a2|+…+|a10|
    =-a1-a2+a3+…+a10
    =（a1+a2+a3+…+a10）-2（a1+a2）
    =10×（-4）+-2（-4-1）
    =105
    故选D
    点评：本题考查数列的求和，解题的关键是弄清数列从第几项起符号发生改变，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    数列{an}中，若
    a
     
    1
    =
    1
    2
    ，an=
    1
    1-an-1
    (n≥2，n∈N)    ，则a2013的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源：广东省六校联合体2012届高三11月联合考试数学文科试题 题型：022

    在数列{an}中，若a－a＝p(n≥2，n∈N*，p为常数)，则{an}称为“等方差数列”，下列是对“等方差数列”的判断：

    ①若{an}是等方差数列，则{a}是等差数列；

    ②{(－1)n}是等方差数列；

    ③若{an}是等方差数列，则{akn}(k∈N*，k为常数)也是等方差数列．

    其中正确命题序号为________．(将所有正确的命题序号填在横线上)

    查看答案和解析>>

    科目：高中数学 来源：湖南师大附中2012届高三第二次月考数学文科试题 题型：022

    在数列{an}中，若a－a＝p(n≥2，n∈N*，p为常数)，则{an}称为“等方差数列”，下列是对“等方差数列”的判断：

    ①若{an}是等方差数列，则{a}是等差数列；

    ②{(－1)n}是等方差数列；

    ③若{an}是等方差数列，则{akn}(k∈N*，k为常数)也是等方差数列．

    其中正确命题序号为________．(将所有正确的命题序号填在横线上)

    查看答案和解析>>

    科目：高中数学 来源：四川省成都市铁路中学2012届高三10月检测数学试题 题型：022

    在数列{an}中，若a－a＝p，(n≥2，n∈N*，p为常数)，则称{an}为“等方差数列”．下列是对“等方差数列”的判断：

    ①若{an}是等方差数列，则{a}是等差数列；

    ②{(－1)n}是等方差数列；

    ③若{an}是等方差数列，则{akn}(k∈N*，k为常数)也是等方差数列；

    ④既是等方差数列、又是等差数列的数列{an}不存在；

    其中正确命题序号为________．(将所有正确的命题序号填在横线上)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在数列{an}中，若a－a＝p(n≥2，n∈N＋，p为常数)，则称{an}为“等方差数列”.下列是对“等方差数列”的判断：

    ①若{an}是等方差数列，则{a}是等差数列；

    ②{(－1)n}是等方差数列；

    ③若{an}是等方差数列，则{akn}(k∈N＋，k为常数)也是等方差数列；

    ④若{an}既是等方差数列，又是等差数列，则该数列为常数数列.

    其中正确命题的序号为　　　　.(将所有正确命题的序号填在横线上).

    查看答案和解析>>

    同步练习册答案