

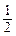 PD=1,
PD=1,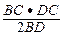 =
=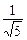 ,
,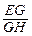 =
=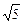 .
.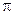 -arctan
-arctan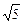 .……………………12分
.……………………12分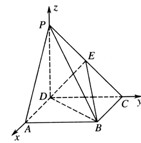
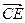 =
=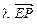 ,则E(0,
,则E(0,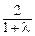 ,
,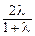 ).
).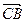 ,a⊥
,a⊥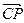 ,
,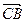 =(1,0,0),
=(1,0,0),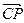 =(0,-2,2),
=(0,-2,2),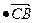 =x1=0,a
=x1=0,a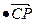 =-2y1+2z1=0,
=-2y1+2z1=0,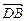 ,b⊥
,b⊥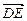 ,
,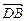 =(1,2,0),
=(1,2,0),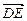 =(0,
=(0,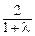 ,
,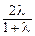 ),
), ∴b
∴b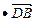 =x2+2y2=0,b
=x2+2y2=0,b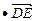 =
=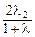 +
+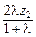 =0,
=0,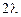 ,
,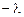 ,1).
,1).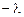 +1=0,
+1=0,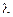 =1.
=1.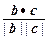 =
=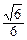 ,
,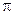 -arccos
-arccos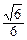 .………………12分
.………………12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
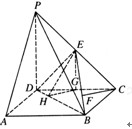
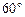 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.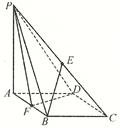
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
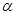 ,
,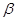 ,
,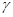 两两互相垂直,点
两两互相垂直,点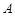 ∈
∈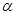 ,点
,点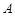 到
到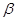 ,
,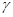 的距离都是
的距离都是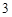 ,点
,点 是
是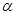 上的动点,满足
上的动点,满足 到
到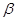 的距离是到
的距离是到 到点
到点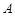 距离的
距离的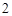 倍,则点
倍,则点 的轨迹上的点到
的轨迹上的点到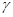 的距离的最小值是
的距离的最小值是A.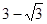 | B.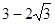 |
C.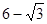 | D.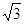 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
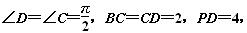 A为PD的中点,如下图,
A为PD的中点,如下图,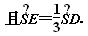
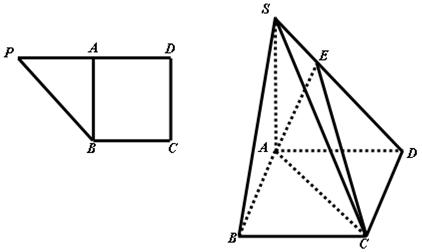
 余弦值;
余弦值; 不存在,请说明理由?
不存在,请说明理由?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
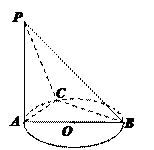 (1)求证:平面PAC⊥平面PBC;
(1)求证:平面PAC⊥平面PBC;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
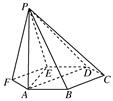
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.30° | B.45° | C.60° | D.90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com