
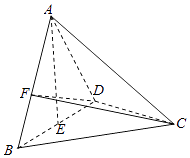
【题目】如图,在三棱锥A﹣BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记 ![]() .
.
(1)当 ![]() 时,求异面直线DF与BC所成角的余弦值;
时,求异面直线DF与BC所成角的余弦值;
(2)当CF与平面ACD所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
【答案】
(1)解:连结CE,以EB、EC、EA分别为x,y,z轴,建立空间直角坐标系,
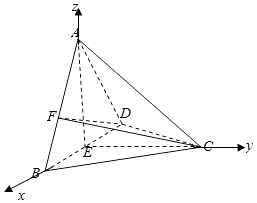
则A(0,0, ![]() ),B(1,0,0),C(0,
),B(1,0,0),C(0, ![]() ,0),D(﹣1,0,0),
,0),D(﹣1,0,0),
∵F是线段AB上一动点,且 ![]() =λ,
=λ,
则 ![]() =
= ![]() =(﹣
=(﹣ ![]() ),∴F(1﹣λ,0,
),∴F(1﹣λ,0, ![]() ),
),
当 ![]() 时,F(
时,F( ![]() ),
), ![]() =(
=( ![]() ),
), ![]() =(1,﹣
=(1,﹣ ![]() ,0),
,0),
∴cos< ![]() ,
, ![]() >=
>= 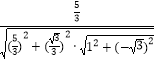 =
= ![]() ,
,
∴异面直线DF与BC所成角的余弦值为 ![]() .
.
(2)![]() =(1﹣
=(1﹣ ![]() ),
), ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(1,
=(1, ![]() ,0),
,0),
设平面ACD的法向量 ![]() =(x,y,z),
=(x,y,z),
则 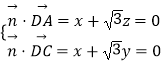 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
∵CF与平面ACD所成角的正弦值为 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
= ![]() ,
,
解得 ![]() 或λ=2(舍),
或λ=2(舍),
∴λ=2.
【解析】(1)根据题意建立空间直角坐标系,用坐标表示直线DF与BC的方向向量,再求得两异面直线的夹角;(2)CF与平面ACD所成角的正弦值等于CF与平面ACD法向量所成角的余弦值.
【考点精析】利用异面直线及其所成的角和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则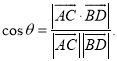 .
.


科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ ![]() 中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+
中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+ ![]() =x求得x=
=x求得x= ![]() .类比上述过程,则
.类比上述过程,则 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.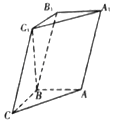
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)E是棱CC1所在直线上的一点,若二面角A﹣B1E﹣B的正弦值为 ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.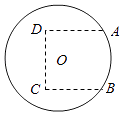
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=
,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED= ![]() ,EC=
,EC= ![]() .则CD= .
.则CD= . 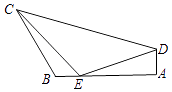
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BCAE=DCAF,B,E,F,C四点共圆.证明:CA是△ABC外接圆的直径.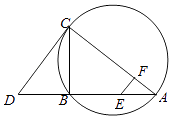
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3 ![]() (1﹣a)x2﹣3ax+1,a>0.
(1﹣a)x2﹣3ax+1,a>0.
(1)试讨论f(x)(x≥0)的单调性;
(2)证明:对于正数a,存在正数p,使得当x∈[0,p]时,有﹣1≤f(x)≤1;
(3)设(1)中的p的最大值为g(a),求g(a)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣a+lnx.
(Ⅰ)若a=1,求证:当x>1时,f(x)>2x﹣1;
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0 , 求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com