
已知函数 (
(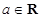 且
且 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)记函数 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数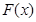 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
(1)函数 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
(2)函数 不存在“中值相依切线”
不存在“中值相依切线”
【解析】本试题主要是考查了导数在研究函数中的运用。利用导数的正负来求解增减区间,并能结合导数的几何意义能解决切线的相关问题。
解:(Ⅰ)显然函数 的定义域是
的定义域是 .
…………1分
.
…………1分
由已知得,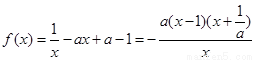 . …………2分
. …………2分
⑴
a>0时, 令 ,解得
,解得 ; 令
; 令 ,解得
,解得 .
.
所以函数 在
在 上单调递增,在
上单调递增,在 上单调递减. ……3分
上单调递减. ……3分
⑵
a<0时, ①当 时,即
时,即 时, 令
时, 令 ,解得
,解得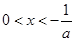 或
或 ;
;
令 ,解得
,解得 .
.
所以,函数 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减; ……4分
上单调递减; ……4分
②当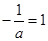 时,即
时,即 时, 显然,函数
时, 显然,函数 在
在 上单调递增;
………5分
上单调递增;
………5分
③当 时,即
时,即 时, 令
时, 令 ,解得
,解得 或
或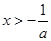 ; 令
; 令 ,解得
,解得 .所以,函数
.所以,函数 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
综上所述,⑴当a>0时,函数 在
在 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;
⑶
a<-1时,函数 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;
⑷
a=-1时,函数 在
在 上单调递增;
上单调递增;
⑸
-1<a<0时,函数 在
在 和
和 上单调递增,在
上单调递增,在 上单调递减. …7分
上单调递减. …7分
(Ⅱ)假设函数 存在“中值相依切线”.
存在“中值相依切线”.
设 ,是曲线
,是曲线 上的不同两点,且
上的不同两点,且 ,
,
则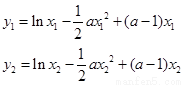 ,
, =
= …8分
…8分
曲线在点 处的切线斜率k=f’(x0)=
处的切线斜率k=f’(x0)=  -a
-a +a-1……9分
+a-1……9分
依题意得:
化简可得:  ,
,
即 . …………11分
. …………11分
设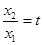 (t>1),上式化为,
(t>1),上式化为, 即
即 . …12分
. …12分
令 ,
,
因为t>1,显然 ,所以
,所以 在
在 上递增,显然有
上递增,显然有 恒成立.
恒成立.
所以在 内不存在
内不存在 ,使得
,使得 成立.
成立.
综上所述,假设不成立.所以,函数 不存在“中值相依切线”.
不存在“中值相依切线”.


科目:高中数学 来源:2014届河北枣强中学高二上学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数 ,且
,且 在
在 和
和 处取得极值.
处取得极值.
(1)求函数 的解析式.
的解析式.
(2)设函数 ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试文科数学 题型:选择题
已知函数 ,且
,且 ,
, .那么下列命题中真命题的序号是
.那么下列命题中真命题的序号是
① 的最大值为
的最大值为 ②
②  的最小值为
的最小值为
③ 在
在 上是减函数
④
上是减函数
④  在
在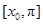 上是减函数
上是减函数
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试文科数学(北京卷) 题型:解答题
(本小题共13分)
已知函数 ,且
,且 是奇函数。
是奇函数。
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)求函数 的单调区间。
的单调区间。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com