(2009年)已知函数f(x)=ax3+3x2-6ax+b,g(x)=3x2+6x+12,h(x)=kx+9,又f(x)在x=2处取得极值9.
(1)求实数a、b的值;
(2)当x∈[-2,+∞)时,f(x)≤h(x)≤g(x)恒成立,求实数k的取值范围.
【答案】
分析:(1)先对函数f(x)进行求导,根据函数f(x)在x=2处取得极值9建立两个等式关系,求出两个变量a,b即可.
(2)由题意知,g(x)=3x
2+6x+12最小值9,f(x)在x=2处取得极值9,h(x)=kx+9的图象是恒过(0,9)的直线,分别作出这三个函数的图象,如图所示,结合图象可知,要使当x∈[-2,+∞)时,f(x)≤h(x)≤g(x)恒成立,只须直线h(x)=kx+9的图象在函数y=f(x)与y=g(x)中间穿过即可,从而得出直线 h(x)=kx+9的斜率k的取值范围.
解答: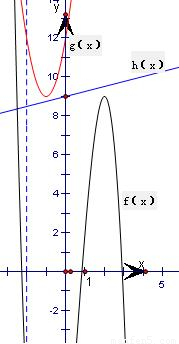
解:(1)∵f′(x)=3ax
2+6x-6a,
由已知
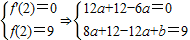
,
解得a=-2,b=-11.
(2)由于g(x)=3x
2+6x+12=3(x+1)
2+9,
故当x=-1时.g(x)取得最小值9;
又由题意知,f(x)在x=2处取得极值9;
h(x)=kx+9的图象是恒过(0,9)的直线,其斜率为k.
分别作出这三个函数的图象,如图所示,
结合图象可知,要使当x∈[-2,+∞)时,f(x)≤h(x)≤g(x)恒成立,
只须直线h(x)=kx+9的图象在函数y=f(x)与y=g(x)中间穿过即可,
此时直线 h(x)=kx+9的斜率大于等于0,
即实数k的取值范围[0,+∞).
点评:本题主要考查了利用导数研究函数的极值、函数恒成立问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

 解:(1)∵f′(x)=3ax2+6x-6a,
解:(1)∵f′(x)=3ax2+6x-6a,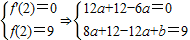 ,
,

 阅读快车系列答案
阅读快车系列答案