
.(本题14分)过点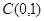 的椭圆
的椭圆 (
(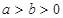 )的离心率为
)的离心率为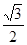 ,椭圆与
,椭圆与 轴的交于两点
轴的交于两点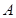 (
(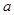 ,
,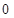 ),
),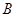 (
(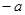 ,
,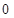 ),过点
),过点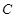 的直线
的直线 与椭圆交于另一点
与椭圆交于另一点 ,并与
,并与 轴交于点
轴交于点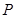 ,直线
,直线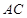 与直线
与直线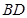 叫与点
叫与点 .
.
(I)当直线 过椭圆右交点时,求线段
过椭圆右交点时,求线段 的长;
的长;
(II)当点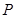 异于
异于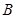 两点时,求证:
两点时,求证: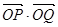 为定值.
为定值.
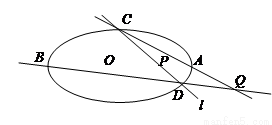
解:(I)由已知得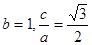 ,解得
,解得
∴ 椭圆方程为
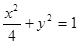 ,--------------------3分
,--------------------3分
右焦点为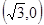 ,直线
,直线 的方程为
的方程为
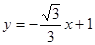 ,
,
代入椭圆方程化简得  ,∴
,∴
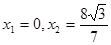 , -------4分
, -------4分
代入直线 的方程得
的方程得  ,
, ,所以,D点坐标为
,所以,D点坐标为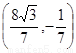 .-------5分
.-------5分
故  -------------------7分
-------------------7分
(II))当直线 与
与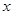 轴垂直时与题意不符,
-------------------8分
轴垂直时与题意不符,
-------------------8分
当直线 与
与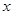 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
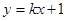 (
( )-------9分
)-------9分
代入椭圆方程化简得  ,
,
解得 ,
,
代入直线 的方程得
的方程得  ,
,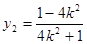
所以,D点坐标为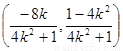 -------------------11分
-------------------11分
又直线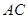 的方程为
的方程为 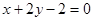 ,直线
,直线 的方程为
的方程为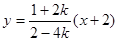
联立解得 ,
-----------------------------13分
,
-----------------------------13分
因此点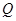 的坐标为(
的坐标为( ),又
),又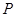 点坐标为(
点坐标为(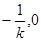 ),
),
所以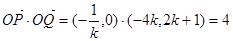
故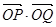 为定值.
-----------------------------14分
为定值.
-----------------------------14分
【解析】略


 快乐5加2金卷系列答案
快乐5加2金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com