
【题目】以平面直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系.已知圆C的极坐标方程为ρ=2sin θ,直线l的参数方程为![]() (t为参数),若l与C交于A,B两点.
(t为参数),若l与C交于A,B两点.
(Ⅰ)求|AB|;
(Ⅱ)设P(1,2),求|PA|·|PB|的值.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ln x,其中a为常数.
(1)当a=-1时,求f(x)的单调递增区间.
(2)当0<-![]() <e时,若f(x)在区间(0,e)上的最大值为-3,求a的值.
<e时,若f(x)在区间(0,e)上的最大值为-3,求a的值.
(3)当a=-1时,试推断方程|f(x)|=![]() 是否有实数根.
是否有实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数y=f(x)满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;②直线x=-4为函数y=f(x)图象的一条对称轴;③函数y=f(x)在[8,10]上单调递增;④若关于x的方程f(x)=m在[-6,-2]上的两根分别为x1,x2,则x1+x2=-8.
其中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知△ABC中,角A,B,C所对的边分别为a,b,c,且3a2+ab-2b2=0.
(Ⅰ)若B=![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若sin A+3sin C=3sin B,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都为正数的数列{an}满足a1=1, ![]() =2an+1(an+1)-an.
=2an+1(an+1)-an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=![]() ,求数列{an·bn}的前n项和Tn.
,求数列{an·bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
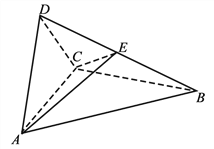
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 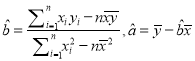 .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.

(Ⅰ)求图中实数a,b的值;
(Ⅱ)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;(Ⅱ)若c=![]() ,△ABC的面积为
,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com