
(14分)已知 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
(Ⅰ)求n的值;
(Ⅱ)求a1+a2+a3+……+an的值.
(Ⅲ) 求 的值。
的值。
(Ⅰ)n=15.(Ⅱ)a1+a2+a3+……+a15=-2.
(Ⅲ)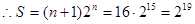
【解析】本题考查二项式定理的应用、二项式系数的性质,解题时要注意排列、组合数的定义、性质,其次注意灵活运用赋值法
(Ⅰ)根据题意,将A 5n=56C 7n
按排列、组合公式展开化简可得(n-5)(n-6)=90,解可得:n=15或n=-4,又由排列、组合数的定义,可得n的范围,即可得答案;
(Ⅱ)由(Ⅰ)中求得n的值,可得(1-2x)15=a0+a1x+a2x2+a3x3+…+a15x15,令x=1可得a0+a1+a2+a3+…+a15=-1,令令x=0得a0=1,两式相减可得答案.
解:(Ⅰ)由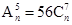 得:
得:
n(n-1)(n-2)(n-3)(n-4)=56 ·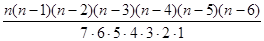
即(n-5)(n-6)=90
解之得:n=15或n=-4(舍去).
∴ n=15.
(Ⅱ)当n=15时,由已知有:
(1-2x)15=a0+a1x+a2x2+a3x3+……+a15x15,
令x=1得:a0+a1+a2+a3+……+a15=-1,
令x=0得:a0=1,
∴a1+a2+a3+……+a15=-2.
(Ⅲ)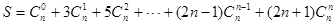
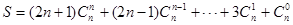

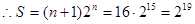


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
1+
| ||||
sin(x+
|
| 3 |
| 5 |
| 3 |
| m |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高二4月段考数学理科试卷(解析版) 题型:解答题
已知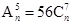 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
(Ⅰ)求n的值;
(Ⅱ)求a1+a2+a3+……+an的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com