
【题目】若圆![]() 关于直线
关于直线![]() 对称,则
对称,则![]() 的最小值为__________.由点
的最小值为__________.由点![]() 向圆所作两条切线,切点记为
向圆所作两条切线,切点记为![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 外接圆的半径为__________.
外接圆的半径为__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).

(1)求这18个数据中不超标数据的平均数与方差;
(2)在空气质量为一级的数据中,随机抽取2个数据,求其中恰有一个为![]() 日均值小于30微克/立方米的数据的概率;
日均值小于30微克/立方米的数据的概率;
(3)以这![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中约有多少天的空气质量超标.
天计算)中约有多少天的空气质量超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装公司生产得到衬衫,每件定价80元,在某城市年销售8万件,现在该公司在该市设立代理商来销售衬衫代理商要收取代销费,代销费为销售金额的![]() %(即每销售100元收取
%(即每销售100元收取![]() 元),为此,该衬衫每件价格要提高到
元),为此,该衬衫每件价格要提高到![]() 元才能保证公司利润.由于提价每年将少销售
元才能保证公司利润.由于提价每年将少销售![]() 万件,如果代理商每年收取的代销费不小于16万元,则
万件,如果代理商每年收取的代销费不小于16万元,则![]() 的取值范围是___________
的取值范围是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足
满足![]() 且
且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
![]() 试判断
试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
![]() 函数
函数![]() 为“
为“![]() 函数”,且当
函数”,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并写出在
的解析式,并写出在![]() 上的单调递增区间;
上的单调递增区间;
![]() 在
在![]() 条件下,当
条件下,当![]() 时,关于
时,关于![]() 的方程
的方程![]() 为常数
为常数![]() 有解,记该方程所有解的和为
有解,记该方程所有解的和为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
停车距离 |
|
|
|
|
|
频数 | 24 | 42 | 24 | 9 | 1 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
(附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为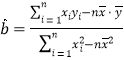 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对下列命题:
①直线![]() 与函数
与函数![]() 的图象相交,则相邻两交点的距离为
的图象相交,则相邻两交点的距离为![]() ;
;
②点![]() 是函数
是函数![]() 的图象的一个对称中心;
的图象的一个对称中心;
③函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 的取值范围为
的取值范围为![]() ;
;
④函数![]() 若
若![]() 对
对![]() R恒成立,则
R恒成立,则![]() .
.
其中所有正确命题的序号为____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com