
分析 (1)利用同角三角函数基本关系式可求sinB,由正弦定理即可求AC的值.
(2)由余弦定理得:AC2-2AC-3=0,即可解得AC,利用三角形面积公式即可求值得解.
解答 解:(1)在△ABC中,BC=$\sqrt{7}$,∠A=60°.
因为cosB=$\frac{\sqrt{6}}{3}$,则sinB=$\frac{\sqrt{3}}{3}$,…(2分)
由正弦定理得:$\frac{AC}{sinB}=\frac{BC}{sinA}$,即$\frac{AC}{\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$,得AC=$\frac{2\sqrt{7}}{3}$,…(5分)
(2)在△ABC中,BC=$\sqrt{7}$,∠A=60°,AB=2.
由余弦定理得:cos∠A=$\frac{A{C}^{2}+4-7}{2×2×AC}$=$\frac{1}{2}$,则AC2-2AC-3=0,
得AC=3.…(8分)
所以△ABC的面积为S=$\frac{1}{2}×2×3×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.…(10分)
点评 本题主要考查了同角三角函数基本关系式,正弦定理,余弦定理,三角形面积公式的综合应用,考查了计算能力和转化思想,属于中档题.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
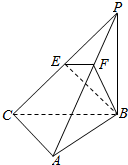 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | 20 | 40 | 70 | 50 | 20 | 200 |
| 女生 | 男生 | 总计 | |
| 及格人数 | 60 | ||
| 不及格人数 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
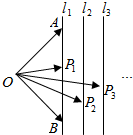 如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.
如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
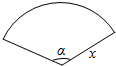 如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.
如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com