Question

 [番茄花园1] 已知m是非零实数，抛物线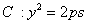（p>0）

的焦点F在直线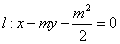上。

（I）若m=2，求抛物线C的方程

（II）设直线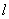与抛物线C交于A、B，△A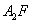,△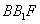的重心分别为G,H

求证：对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。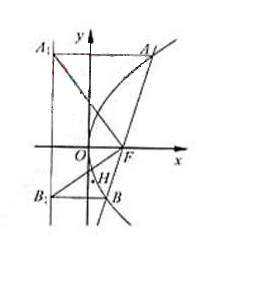

 

---

 [番茄花园1]1.

Answer 1

【答案】

 [番茄花园1] .解析：本题主要考查抛物线几何性质，直线与抛物线、点与圆的位置关系等基础知识，同时考查解析几何的基本思想方法和运算求解能力。

(Ⅰ)解：因为焦点F(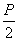,0)在直线l上，

得

又m=2,故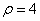

所以抛物线C的方程为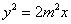

设A(x₁,y₁) ,  B(x_2,y₂)

由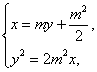消去x得

ym³y－m⁴＝0，

由于m≠0，故＝4m⁶＋4m⁴＞0，

且有y₁＋y₂＝2m³，y₁y₂＝－m⁴，

设M₁，M₂分别为线段AA₁，BB₁的中点，

由于2

可知G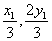（），H（），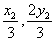

所以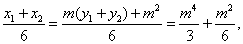

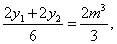
    所以GH的中点M.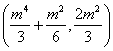

设R是以线段GH为直径的圆的半径，

则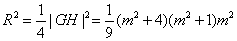

设抛物线的标准线与x轴交点N，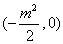

则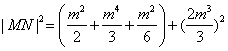

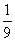=m⁴(m⁴+8 m²+4)

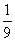=m⁴[(m²+1)( m²+4)+3m²]

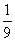＞m² (m²+1)( m²+4)=R².

故N在以线段GH为直径的圆外.

 

 

---

 [番茄花园1]22.