
分析 求导f′(x)=ex(x-2a)(x-2),分类讨论从而可得f(x)的单调性.
解答 解:∵f(x)=ex(x2-(2a+4)x+6a+4),
∴f′(x)=ex(x2-(2a+4)x+6a+4+2x-(2a+4))
=ex(x2-(2a+2)x+4a)
=ex(x-2a)(x-2),
①当2a<2,即a<1时,
故当x∈(-∞,2a)∪(2,+∞)时,f′(x)>0;
当x∈(2a,2)时,f′(x)<0;
故f(x)在(-∞,2a),(2,+∞)上单调递增,
在(2a,2)上单调递减;
②当2a=2,即a=1时,
故当x∈(-∞,2)∪(2,+∞)时,f′(x)>0;
故f(x)在(-∞,+∞)上单调递增;
③当2a>2,即a>1时,
故当x∈(-∞,2)∪(2a,+∞)时,f′(x)>0;
当x∈(2,2a)时,f′(x)<0;
故f(x)在(-∞,2),(2a,+∞)上单调递增,
在(2,2a)上单调递减.
点评 本题考查了导数的综合应用及分类讨论的思想应用.


科目:高中数学 来源: 题型:填空题
 设函数f(x)=|x2-2x|(x∈R).
设函数f(x)=|x2-2x|(x∈R).| x | … | -2 | 0 | 1 | 2 | 3 | … |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
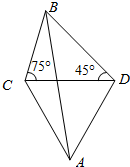 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)≠0且g(x)≠0 | B. | ?x∈R,f(x)≠0或g(x)≠0 | ||
| C. | ?x0∈R,f(x0)≠0且g(x0)≠0 | D. | ?x0∈R,f(x0)≠0或g(x0)≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3},1$] | B. | ($\frac{2}{3},1$] | C. | [$\frac{2}{3},1$) | D. | ($\frac{2}{3},1$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com