
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
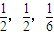 根据甲、乙、丙三地实施的人工降雨彼此互不影响,这三种情况是互斥的,得到甲、乙、丙三地都恰为中雨的概率.
根据甲、乙、丙三地实施的人工降雨彼此互不影响,这三种情况是互斥的,得到甲、乙、丙三地都恰为中雨的概率.
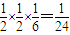
 ,
,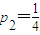 ,
,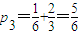 ,
,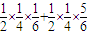 +
+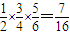


科目:高中数学 来源: 题型:
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 摸拟试验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源:2012届度湖南省高三下学期二轮复习理科数学试卷 题型:解答题
某研究小组在电脑上进行人工降雨摸拟试验,准备用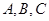 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下:
|
方式 |
实施地点 |
大雨 |
中雨 |
小雨 |
摸拟试验总次数 |
|
|
甲 |
4次 |
6次 |
2次 |
12次 |
|
|
乙 |
3次 |
6次 |
3次 |
12次 |
|
|
丙 |
2次 |
2次 |
8次 |
12次 |
假设甲、乙、丙三地实施的人工降雨彼此互不影响.
(Ⅰ)求甲、乙两地恰为中雨且丙地为小雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即能达到理想状态,乙地必须是大雨才能达到理想状态,丙地只要是小雨或中雨就能达到理想状态,求甲、乙、丙三地中至少有两地降雨量达到理想状态的概率.
查看答案和解析>>
科目:高中数学 来源:2012年高三二轮复习综合验收数学试卷2(理科)(新课标)(解析版) 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 摸拟试验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com