练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，有acosA＋bcosB＝ccosC，试判断△ABC的形状．

    (和差化积公式：sinA＋sinB＝2sin)

    答案：
    解析：

    　　

    　　[点评]判断三角形的形状，应围绕三角形的边角关系进行思考，主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形、锐角三角形，要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别，依据已知条件中的边角关系判断时，主要有如下两条途径：

    　　(1)利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；

    　　(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数的恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A＋B＋C＝π这个结论．

    　　(3)在两种解法的等式变形中，一般两边不要约去公因式，应移项提取公因式，以免漏解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    14、在平面几何中，有射影定理：“在△ABC中，AB⊥AC，点A在BC边上的射影为D，有AB2=BD•BC．”类比平面几何定理，研究三棱锥的侧面面积与射影面积、底面面积的关系，可以得出的正确结论是：“在三棱锥A-BCD中，AD⊥平面ABC，点A在底面BCD上的射影为O，则有
    S△ABC2=S△BCO•S△BCD

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，有命题
    ①
    AB
    -
    AC
    =
    BC
    ；
    ②
    AB
    +
    BC
    +
    CA
    =
    0
    ；
    ③若(
    AB
    +
    AC
    )•(
    AB
    -
    AC
    )=0    ，则△ABC为等腰三角形；
    ④若
    AC
    •
    AB
    ＞0    ，则△ABC为锐角三角形．
    上述命题正确的是（　　）
    A、①②B、①④C、②③D、②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，PA⊥平面ABC，在△ABC中，BC⊥AC，则图中有
    4
    4
    个直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，有命题：
    ①
    AB
    -
    AC
    =
    BC
    ；
    ②
    AB
    +
    BC
    +
    CA
    =
    0
    ；
    ③若(
    AB
    +
    AC
    )•(
    AB
    -
    AC
    )=0    ，则△ABC为等腰三角形；
    ④若
    AC
    •
    AB
    ＜0    ，则△ABC为钝角三角形．
    上述命题正确的是（　　）
    A、①②B、①④C、②③D、②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

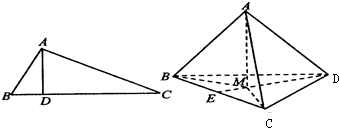    精英家教网如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2=BD•BC；类似地有命题：在三棱锥A-BCD中，AD⊥面ABC，若A点在BCD内的射影为M，则有
    S
    2
    △ABC
    =S△BCM•S△BCD    ．上述命题是（　　）

    查看答案和解析>>

    同步练习册答案