
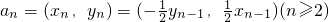
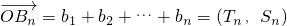 (O是坐标原点),求Sn
(O是坐标原点),求Sn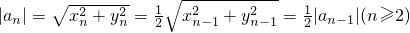 ,
,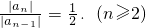
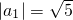 ,∴{|an|}是首项为
,∴{|an|}是首项为 .公比为
.公比为 的等比数列.(4分)
的等比数列.(4分)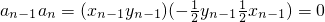 ,∴an-1与an的夹角θ=90°(6分)
,∴an-1与an的夹角θ=90°(6分)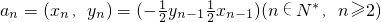 ,得
,得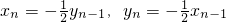 .
.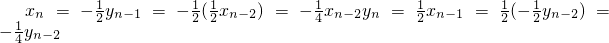 ,
,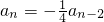 ,∴
,∴ ,
,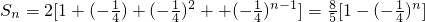 (12分)
(12分)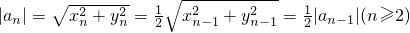 ,通过
,通过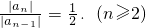 符合等比数列的定义可证,但要注意明确首项和公比.
符合等比数列的定义可证,但要注意明确首项和公比.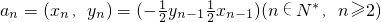 ,得
,得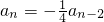 ,从而有
,从而有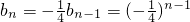 再由等比数列前n项和公式求解.
再由等比数列前n项和公式求解.

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:成都一模 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年广东省汕头市高考数学一模试卷(文科)(解析版) 题型:解答题
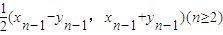
查看答案和解析>>
科目:高中数学 来源:2013年四川省成都市高三12月一诊试卷(理科)(解析版) 题型:解答题
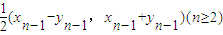
查看答案和解析>>
科目:高中数学 来源:2012年广东省汕头市高三毕业班教学质量检测数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com