
现有编号分别为1,2,3,4,5,6,7, 8,9的九道不同的数学题。某同学从这九道题中一次随机抽取两道题,每题被抽到的概率是相等的,用符号 表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”.
(1)共有多少个基本事件?并列举出来;
(2)求该同学所抽取的两道题的编号之和小于17但不小于11的概率.
(1)共36个基本事件,详见解析;(2)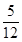 .
.
解析试题分析:(1)从前往后依次取编号组成数对,注意不能出现重复,也不能遗漏;(2)从(1)中找出编号之和小于17但不小于11的基本事件,由古典概型的计算公式,与总的基本事件个数相除即可得概率.
试题解析:
解:(1)共36个基本事件:
(1,2);(1,3);(1,4);(1,5);(1,6);(1,7);(1,8);(1,9);(2,3);
(2,4);(2,5);(2,6);(2,7);(2,8);(2,9);(3,4);(3,5);(3,6);
(3,7);(3,8);(3,9);(4,5);(4,6);(4,7);(4,8);(4,9);(5,6);
(5,7);(5,8);(5,9);(6,7);(6,8);(6,9);(7,8);(7,9);(8,9). 5分
(2) 该同学所抽取的两道题的编号之和小于17但不小于11包含:
(2,9);(3,8);(3,9);(4,7);(4,8);(4,9);(5,6);
(5,7);(5,8);(5,9);(6,7);(6,8);(6,9);(7,8);(7,9)15个基本事件
所以该同学所抽取的两道题的编号之和小于17但不小于11的概率为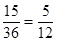 . 10分
. 10分
考点:古典概型的概率计算.


科目:高中数学 来源: 题型:解答题
甲乙两人进行掰手腕比赛,比赛规则规定三分钟为一局,三分钟内不分胜负为平局,当有一人赢3局就结束比赛,否则继续进行,根据以往经验,每次甲胜的概率为 ,乙胜的概率为
,乙胜的概率为 ,且每局比赛胜负互不受影响.
,且每局比赛胜负互不受影响.
(Ⅰ)求比赛4局乙胜的概率;
(Ⅱ)求在2局比赛中甲的胜局数为ξ的分布列和数学期望;
(Ⅲ)若规定赢一局得2分,平一局得1分,输一局得0分,比赛进行五局,积分有超过5分者比赛结束,否则继续进行,求甲得7分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知方程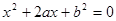 是关于
是关于 的一元二次方程.
的一元二次方程.
(1)若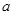 是从集合
是从集合 四个数中任取的一个数,
四个数中任取的一个数,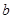 是从集合
是从集合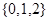 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率;
(2)若 ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
(1)若甲、乙两个小组的数学平均成绩相同,求a的值;
(2)求乙组平均成绩超过甲组平均成绩的概率;
(3)当a=2时,分别从甲、乙两组中各随机选取一名同学,设这两名同学成绩之差的绝对值为X,求随机变量X的分布列和数学期望,
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)把一颗质地均匀,四个面上分别标有复数 ,
,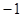 ,
,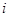 ,
,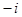 (
(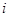 为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为
为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为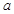 ,第二次出现底面朝下的复数记为
,第二次出现底面朝下的复数记为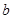 .
.
(1)用 表示“
表示“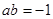 ”这一事件,求事件
”这一事件,求事件 的概率
的概率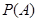 ;
;
(2)设复数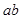 的实部为
的实部为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4.
(1)从箱子中任取两张卡片,求两张卡片的标号之和不小于5的概率;
(2)从箱子中任意取出一张卡片,记下它的标号 ,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号
,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号 ,求使得幂函数
,求使得幂函数 图像关于
图像关于 轴对称的概率.
轴对称的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com