
 ,
, 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且 =x
=x +y
+y (x,y∈R),则x2+y2的最小值为( )
(x,y∈R),则x2+y2的最小值为( )




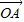 |=|
|=|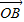 |=1时,建立直角坐标系,得x+y=
|=1时,建立直角坐标系,得x+y= ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;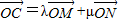 ,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=
,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=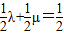 ,下同法一
,下同法一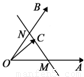 解法一:特殊值法,当θ=90°,|
解法一:特殊值法,当θ=90°,|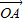 |=|
|=|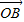 |=1时,建立直角坐标系,
|=1时,建立直角坐标系,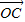 =x
=x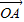 +y
+y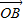
 ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;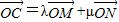 ,有λ+μ=1,
,有λ+μ=1, =
=
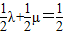
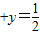 时,求x2+y2的最小值问题,
时,求x2+y2的最小值问题,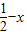
 =
=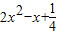
 时,取得最小值为
时,取得最小值为
 ,有λ+μ=1“的应用
,有λ+μ=1“的应用 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
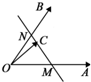 如图所示,两个非共线向量
如图所示,两个非共线向量| OA |
| OB |
| OC |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.1平面向量的实际背景及其基本概念(解析版) 题型:解答题
如图所示,4×3的矩形(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问:
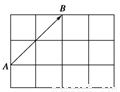
(1)与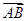 相等的向量共有几个;
相等的向量共有几个;
(2)与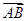 平行且模为
平行且模为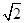 的向量共有几个?
的向量共有几个?
(3)与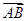 方向相同且模为3
方向相同且模为3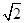 的向量共有几个?
的向量共有几个?
[分析] 非零向量平行(共线)包括两种情况:一种是方向相同,另一种是方向相反.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如图所示,两个非共线向量
如图所示,两个非共线向量 ,
, 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且 =x
=x +y
+y (x,y∈R),则x2+y2的最小值为
(x,y∈R),则x2+y2的最小值为



查看答案和解析>>
科目:高中数学 来源:2012年陕西省高考数学压轴卷(解析版) 题型:选择题
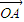 ,
,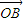 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且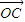 =x
=x +y
+y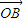 (x,y∈R),则x2+y2的最小值为( )
(x,y∈R),则x2+y2的最小值为( )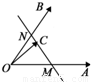
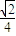

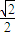

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com